Seminararbeit
Evaluation & Forschungsmethodik
Dozent: Prof. Dr. Joachim Werner
Psychologisches Institut
Universität Heidelberg
WS 1996/97
2. Das allgemeine lineare Modell (ALM)
4. Dummycodierung mit Covariate
In der modernen sozialwissenschaftlichen Forschung hat sich zunehmend die Erkenntnis durchgesetzt, daß der Komplexität menschlichen Verhaltens und Erlebens in vielen Fällen nur multivariate Ansätze gerecht werden. Diese erlauben es, mehrere Variablen gleichzeitig zu erheben und auszuwerten. So läßt sich beispielsweise mithilfe der multiplen Regressionsrechnung der Einfluß vieler Prädiktorvariablen auf eine Kriteriumsvariable durch eine einzige Gleichung abbilden. Bei diesem Verfahren läßt sich die jeweilige Gewichtung der einzelnen in die Gleichung einbezogenen Variablen leicht feststellen. Eine der Voraussetzungen, die vor Anwendung der Regressionsrechnung sicherzustellen ist, besteht in der Intervallskalierung der beteiligten Variablen. Das allgemeine lineare Modell gibt hierbei dem Forscher ein Instrument an die Hand, das es erlaubt, die unterschiedlichsten Variablen mit der multiplen Regression zu behandeln. Kategoriale Variablen müssen dabei zunächst durch ein besonderes Codierungsverfahren in Intervallskalierung überführt werden und lassen sich sodann mit der Korrelationsrechnung behandeln.
So könnte beispielsweise in einer Studie zu den Determinanten sozialer Kompetenz der Zusammenhang zwischen Persönlichkeitsmerkmalen und sozialer Kompetenz untersucht werden. Will der Forscher nun erfahren, welchen Varianzanteil im Vergleich zu den anderen Variablen die Geschlechtszugehörigkeit aufklärt, so könnte er das Merkmal H3Geschlecht" nach entsprechender Codierung mit in die Regressionsgleichung als Prädiktor einbeziehen.
Dies impliziert zum einen eine erhebliche Vereinfachung, da Teilbereiche der gleichen Fragestellung nun nicht mehr mit getrennten statistischen Verfahren zu behandeln sind, zum anderen lassen sich durch die metrische Skalierung multidimensionale Beziehungszusammenhänge zwischen den Variablen untersuchen, wo vorher lediglich mehrfaktorielle Varianzanalysen möglich waren. Ist bei einem oder zwei Faktoren in der Regel die Varianzanalyse das Verfahren der Wahl, so ergibt sich mit steigender Faktorenzahl das Problem der Überdeterminierung, da die Zahl der zu untersuchenden Wechselwirkungen rasch zunimmt. Auch wird häufig auf einen globalen Signifikanztest für das gesamte Modell verzichtet, so daß sich bei beliebig vielen Faktoren rasch aufgrund des Kumulierungseffektes signifikante Ergebnisse einstellen. Bei Verwendung der multiplen Regressionsrechnung läßt sich die Vorhersagequalität des gesamten Modells leicht anhand des multiplen Korrelationskoeffizienten bestimmen und inferenzstatistisch absichern.
In der vorliegenden Arbeit soll am Beispiel erläutert werden, wie kategoriale Variablen durch Dummycodierung einem regressionsanalytischen Ansatz zugänglich gemacht werden können und somit ein eigentlich varianzanalytisches Design durch eine Regressionsgleichung ausgedrückt werden kann.
Bortz (1993) führt zur Intention des allgemeinen linearen Modells aus:
H3Das allgemeine lineare Modell integriert die wichtigsten Verfahren der Elementarstatistik, varianzanalytische Verfahren sowie die multiple Korrelations- und Regressionsrechnung".
Die Idee, auf welcher das ALM basiert, ist die additiv-lineare Verknüpfbarkeit der Parameter. Nichtlineare Komponenten sind dabei vorher entsprechend mathematisch zu substituieren. Die für das ALM angewandte inferenzstatistische Methode ist die der multiplen Regression.
Der Meßwert der Kriteriumsvariablen y (AV) für Versuchsperson i bei k Prädiktoren (UVs) läßt sich wie folgt definieren:
![]()
x1i...ki sind die Prädiktorwerte der i-ten Versuchsperson in der Variablen 1...k
b1...k sind die errechneten Regressionsgewichte der Gleichung
a steht für die Regressionskonstante in der Gleichung
ei ist der individuelle Fehlerwert der Versuchsperson i.
Je nach Stärke des multiplen Zusammenhang ist die Schätzung von y aus den Prädiktorvariablen unterschiedlich genau, was sich im Determinationskoeffizienten R2 niederschlägt, welcher der multiplen Korrelation zwischen den Prädiktoren und dem Kriterium entspricht.
Bei der Interpretation der standardisierten Betagewichte ist zu beachten, daß die Prädiktoren mehr oder weniger stark korreliert sein können (Multikollinearität). Die quadrierten Betagewichte addieren sich in ihrer Varianzaufklärung des Kriteriums also nicht.
Abbildung 1: Venndiagramm zur Veranschaulichung des Multikollinearitätsproblems.
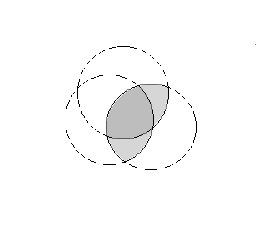 |
Im dunkelgrau schattierten Bereich überlagern sich die von x1 und x2 an y aufgeklärten Varianzanteile, so daß hier keine Additivität gegeben ist. |
Die zunehmende Anwendung des ALM in den letzten Jahren ist sicherlich zum Teil auch auf die wachsende Verfügbarkeit leistungsstarker Computer und Statistikprogramme zurückzuführen, da die Berechnung von multiplen Korrelationskoeffizienten und Regressionsgleichungen mit vielen Variablen mit einem erheblichen Rechenaufwand verbunden ist. Leider korrespondiert die heutige Verfügbarkeit der entsprechenden Rechenkapazität nicht immer mit den entsprechenden Methoden- und Statistikkenntnissen seitens des Anwenders. Die Regressionsrechnung reagiert empfindlich auf Verletzungen ihrer Grundvoraussetzungen, was unter Umständen zu ineffizienten inferenzstatistischen Schätzungen der Parameter und damit irreführenden Ergebnissen führen kann. Eine sorgfältige Versuchsplanung und -durchführung ist sicherlich eine notwendige, nicht aber immer eine hinreichende Bedingung, um die Voraussetzungen für die Anwendung des linearen Modells zu gewährleisten. Aus diesem Grund sollten grundsätzlich entsprechende Nachtests anhand der Regressionsresiduen vorgenommen werden und ernste Verletzungen der Bedingungen des ALM auf ihre Ursachen hin untersucht werden. Werner (1997) nennt sechs Voraussetzungen des allgemeinen linearen Modells, deren Erfüllung bzw. Verletzung graphisch durch Residualplots und, bei größeren Stichproben, auch inferenzstatistisch getestet werden sollte:
1. Unabhängigkeit der Fehler
2. Homoskedaszität
3. Linearität
4. Spezifikation der Prädiktoren
5. Ausreißer
6. Normalität der Fehlerverteilung
Probleme können sich auch ergeben, wenn die Prädiktoren untereinander stark korreliert sind, was die Stabilität der Betagewichte in der Gleichung gefährdet und die Interpretation erschwert (Multikollinearität, siehe Abb. 1).
Werner (1997) nennt drei Codierungsverfahren, mit denen nominalskalierte Variablen verschlüsselt werden können:
1. Dummycodierung
2. Effektcodierung
3. Orthogonalcodierung
Allen Verfahren ist dabei gemeinsam, daß ein p-fach gestuftes nominales Merkmal durch (p-1) Indikatorvariablen ersetzt wird. In der vorliegenden Arbeit sollen Dummy- und Effektcodierung am Beispiel erläutert werden.
Diese Form der Codierung wird angewandt, wenn eine bis mehrere Treatmentgruppen mit einer Kontrollgruppe verglichen werden sollen. Im gewählten Beispiel (entnommen und erweitert aus: Werner, Lineare Statistik, 1997, S. 215) wird untersucht, ob zwei neue Lehrmethoden die Lernleistungen der Probanden im Vergleich mit einer Kontrollgruppe, die nach der alten Methode unterrichtet wird, verbessern. Zunächst erfolgt die Auswertung mit einem varianzanalytischen Design, wie bei derartigen inferenzstatistischen Fragestellungen üblich:
Tabelle 1: Datenschema einfaktorielle Varianzanalyse
Bedingung |
Methode 1 |
Methode 2 |
Kontrollgruppe |
|
Lernleistung der Vpn |
1 2 3 |
7 8 6 |
5 3 1 |
|
Mittelwerte |
MW = 2 |
MW = 7 |
MW = 3 |
MW = 4 |
Tabelle 2: Einfaktorielle Varianzanalyse
|
Variable LERNLEISTUNG By Variable METHODE |
|||||
| Analysis of Variance | |||||
| Source> | D.F. | Sum of Squares | Mean Squares | F Ratio | F Prob. |
| Between Groups | 2 | 42.0000 | 21.0000 | 10.5000 | .0110 |
| Within Groups | 6 | 12.0000 | 2.0000 | ||
| Total | 8 | 54.0000 | |||
| R-Quadrat=0,778 |
Es liegt ein signifikanter Haupteffekt vor, wobei 77 % der Gesamtvarianz auf Unterschiede zwischen den Gruppen zurückgeht.
Ein Nachtest nach Scheffe ergibt, daß sich die Ergebnisse der nach Methode 2 unterrichteten Gruppen von denen der Kontrollgruppe signifikant unterscheiden. Die nach Methode 1 unterrichtete Gruppe erzielt keine signifikant besseren Ergebnisse als die Kontrollgruppe. (Außerdem sind die Ergebisse von Gruppe 2 signifikant besser als diejenigen von Gruppe 1).
Es erfolgt nun die Umsetzung des Problems in das allgemeine lineare Modell:
Tabelle 3: Dummycodierung bei einfaktorieller Varianzanalyse
Bedingung |
y - Lernleistung |
x1 |
x2 |
Methode 1 |
1 2 3 |
1 1 1 |
0 0 0 |
Methode 2 |
7 8 6 |
0 0 0 |
1 1 1 |
Kontrollgruppe |
5 3 1 |
0 0 0 |
0 0 0 |
Jeder der drei Gruppen kann mit zwei Dummyvariablen ein eindeutiges Codemuster zugeordnet werden. Bei Dummycodierung wird grundsätzlich mit null und eins codiert. Die Referenz- bzw. Kontrollgruppe ist auf beiden Variablen mit null zu codieren. Die so gewonnenen Dummyvariablen x1 und x2 werden als unabhängige Variablen in eine lineare Regression (Tabelle 4) eingeführt, die abhängige Variable in diesem Modell ist die Lernleistung.
Die Betakoeffizienten der Regressionsgleichung im vorliegenden Fall errechnen sich wie folgt:
![]()
Bekannt sind die Gruppenmittelwerte von y unter den drei Bedingungen mit
![]()
Für die dritte Bedingung als Referenzgruppe wurde folgende Codierung gewählt:
![]()
So vereinfacht sich die Regressionsgleichung unter der dritten Bedingung wie folgt:
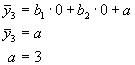
Damit entspricht die Regressionskonstante dem Mittelwert der Kontrollgruppe. Dieser wird in die Regressionsgleichung eingesetzt:
![]()
Für die erste Bedingung wurde folgende Codierung gewählt:
![]()
Damit ergibt sich:
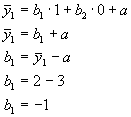
Codierung unter der zweiten Bedingung:
![]()
Einsetzen in die Regressionsgleichung ergibt:
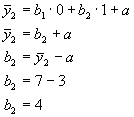
Vollständige unstandardisierte Regressionsgleichung für das verwendete Beispiel:
![]()
Interpretation der Regressionsparameter im SPSS-Output:
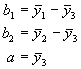
Ein Blick auf Tabelle 4 zeigt, daß die Regression als Ganzes signifikant ist (p=.011). Auch Quadratsummen sowie R2 (0,77) entsprechen den Werten bei der Varianzanalyse. Die Signifikanzaussagen über die Betagewichte beziehen sich somit auf den Vergleich der ersten beiden Gruppen mit der Kontrollgruppe. Der Mittelwertsunterschied zwischen Gruppe eins und Gruppe drei (2-3=-1) ist mit p=.4198 nicht signifikant. Der Vergleich von Gruppe zwei mit Gruppe drei (7-3=4) ist mit p=.0134 im gewählten Beispiel signifikant.
Tabelle 4: Multiple Regression bei Dummycodierung
|
Multiple R .88192 R Square .77778 Adjusted R Square .70370 Standard Error 1.41421 |
|||
| Analysis of Variance | |||
| DF | Sum of Squares | Mean Square | |
| Regression | 2 | 42.00000 | 21.00000 |
| Residual | 6 | 12.00000 | 2.00000 |
| F = 10.50000 Signif F = .0110 | |||
------------------ Variables in the Equation ------------------
| Variable | B | SE B | Beta | T | Sig T |
| X1 | -1.000000 | 1.154701 | -.192450 | -.866 | .4198 |
| X2 | 4.000000 | 1.154701 | .769800 | 3.464 | .0134 |
| (Constant) | 3.000000 | .816497 | 3.674 | .0104 |
Damit ist anzumerken, daß die Regressionskoeffizienten nur interpretierbar sind, wenn die gewählte Kodierung bekannt ist." (Werner, 1997).
Der Vorteil dieses Verfahrens besteht offentsichtlich darin, daß sich weitere unabhängige Variablen problemlos in die Gleichung mit aufnehmen lassen, um mehr Varianz aufklären zu können.
Dummycodierung bei zwei Faktoren
Ein varianzanalytisches Design mit p x q Stufen benötigt (p-1) Dummyvariablen für den ersten Faktor, (q-1) Dummyvariablen für den zweiten Faktor sowie (p-1)(q-1) Dummys für die Wechselwirkung zwischen den zwei Faktoren. Die Codierung der Wechselwirkung ist dabei einfach durchzuführen, indem die Hauptdummys elementeweise multipliziert werden.
Beispiel: In einer Studie zum Erfolg verschiedener Therapieverfahren wird nach einem Jahr eine Katamnese durchgeführt. Zugleich wird erhoben, ob während des Katamnesezeitraumes eine Selbsthillfegruppe besucht wurde oder nicht.
Tabelle 5: Datenschema zur zweifaktoriellen Varianzanalyse
Verfahren 1 |
Verfahren 2 |
Kontrollgruppe |
||
Selbsthilfegruppe ja |
a1b1 |
a2b1 |
a3b1 |
b1 |
Selbsthilfegruppe nein |
a1b2 |
a2b2 |
a3b2 |
b2 |
a1 |
a2 |
a3 |
x4 ergibt aus der Multiplikation von x1 mit x3,
x5 erhält man aus der Multiplikation von x2 mit x3.
Tabelle 6: Dummycodierung bei zweifaktorieller Varianzanalyse (3 x 2 - Design)
Faktor A |
Faktor B |
Wechselwirkung A x B | |
x1 x2 |
x3 |
x4 x5 | |
a1b1 a1b2 a2b1 a2b2 a3b1 a3b2 |
1 0 1 0 0 1 0 1 0 0 0 0 |
1 0 1 0 1 0 |
1 0 0 0 0 1 0 0 0 0 0 0 |
Zu beachten ist allerdings, daß die Interpretation der Betakoeffizienten bei Einbeziehung von Wechselwirkungseffekten nicht unproblematisch ist und eine eingehende Vertrautheit mit der Materie voraussetzt, ein erschöpfendes Eingehen auf diese Thematik ist an dieser Stelle aus Platzgründen nicht möglich.
Diese Form der Codierung kommt zum Einsatz, wenn von Interesse ist, welche Gruppenmittelwerte sich signifikant vom Gesamtmittelwert unterscheiden. Dieses Vorgehen entspricht der varianzanalytischen Idee. So wird im einfaktoriellen varianzanalytischen Modell beim globalen Signifikanztest untersucht, ob sich mindestens ein Gruppenmittelwert signifikant vom Gesamtmittelwert unterscheidet. Die Summe der Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert muß dabei immer Null ergeben.
Bei der Effektcodierung ergibt sich damit die Forderung, daß sich die Werte jeder Codiervariablen über die einzelnen Stufen hinweg zu null addieren müssen. Dies kann nur durch Verwendung sowohl positiver als auch negativer Zahlen erreicht werden: Anstatt die Kontrollbedingung mit null zu codieren, wird diese durchgängig mit -1 codiert.
Tabelle 7: Effektcodierung bei einfaktorieller Varianzanalyse
Bedingung |
y - Lernleistung |
x1 |
x2 |
Methode 1 |
1 2 3 |
1 1 1 |
0 0 0 |
Methode 2 |
7 8 6 |
0 0 0 |
1 1 1 |
Kontrollgruppe |
5 3 1 |
-1 -1 -1 |
-1 -1 -1 |
Ein Blick auf Tabelle 6 zeigt, daß die globalen Werte der multiplen Regression unverändert sind. Allerdings bringt die Effektcodierung bei den b-Gewichten andere Ergebnisse hervor als die Dummycodierung. Dies ergibt sich daraus, daß sich bei der Effektcodierung die Betagewichte anders bestimmen. Anhand eines Gleichungssystems mit drei Unbekannten lassen sich Regressionskonstante sowie Betagewichte leicht bestimmen:
y= b1x1+b2x2+ a
y3= 3=-b1 -b2 + a (1)
y1= 2= b1 + a (2)
y2= 7= b2 + a (3)
-----------------------------------
12= 3a (4)=(1)+(2)+(3)
4= a (5)=(4)/3
-----------------------------------
2= b1 + 4 (6)=(5)in(2)
-2= b1 (7)
-----------------------------------
7= b2 + 4 (8)=(5)in(3)
3= b2 (9)
-----------------------------------
Tabelle 8: Multiple Regression bei Effektcodierung
|
Multiple R .88192 R Square .77778 Adjusted R Square .70370 Standard Error 1.41421 |
|||
| Analysis of Variance | |||
| DF | Sum of Squares | Mean Square | |
| Regression | 2 | 42.00000 | 21.00000 |
| Residual | 6 | 12.00000 | 2.00000 |
| F = 10.50000 Signif F = .0110 |
------------------ Variables in the Equation ------------------
| Variable | B | SE B | Beta | T | Sig T |
| X1 | -2.000000 | .666667 | -.666667 | -3.000 | .0240 |
| X2 | 3.000000 | .666667 | 1.000000 | 4.500 | .0041 |
| (Constant) | 4.000000 | .471405 | 8.485 | .0001 |
Die Konstante der Regressionsgleichung ist nun mit dem Gesamtmittelwert über alle drei Gruppen identisch, was sich aus Gleichung (4) ergibt. b1 gibt die Abweichung des Mittelwertes von Gruppe eins an (4-2=2). b2 gibt die Abweichung des Mittelwertes von Gruppe zwei an (4+3=7). Beide Gruppenmittelwerte weichen mit p=.0240 bzw. p=.0001 signifikant vom Gesamtmittelwert ab (Anmerkung: Bei der Dummycodierung wurde mit dem Mittelwert von Gruppe drei, der Kontrollgruppe, verglichen). Die Kontrollgruppe taucht als Referenzgruppe auch hier in der Gleichung nicht auf.
Interpretation der Regressionsparameter im SPSS-Output:
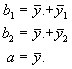
Effektcodierung bei zwei Faktoren
Tabelle 9: Effektcodierung bei zweifaktorieller Varianzanalyse (3 x 2 - Design)
Faktor A |
Faktor B |
Wechselwirkung A x B | |
x1 x2 |
x3 |
x4 x5 | |
a1b1 a1b2 a2b1 a2b2 a3b1 a3b2 |
1 0 1 0 0 1 0 1 -1 -1 -1 -1 |
1 -1 1 -1 1 -1 |
1 0 -1 0 0 1 0 -1 -1 -1 1 1 |
Bei Dummy- und Effektcodierung sind die einzelnen Codiervektoren miteinander korreliert. Werner (1997) führt als dritte Codierungsmethode noch die Orthogonalcodierung an, welche voneinander unabhängige Codiervektoren liefert und so durchgeführt wird, daß das Skalarprodukt der Vektoren gleich null ist.
Um die integrierende Funktion des ALM zu demonstrieren, soll nun untersucht werden, wie sich die Regressionsgleichung verändert, sobald eine intervallskalierte Covariate in das Modell miteinbezogen wird. Für das eingangs erwähnte Beispiel soll angenommen werden, daß zusätzlich die Lernmotivation der Probanden erfaßt wurde. Tabelle 11 zeigt, daß sich Lernmethode 2 immer noch signifikant von der Kontrollgruppe unterscheidet bei Einbeziehung der Lernmotivation in das Modell. Diese wäre für sich genommen ebenfalls signifikant (p=.0182) und vom Gewicht her fast ebenso bedeutsam wie die Gruppendifferenz (Beta = .588). Gleichzeitig ist die Gesamtaufklärung der Varianz auf R2 = 0,934 gestiegen, das Modell als Ganzes ist nach wie vor signifikant (p=.0022).
Tabelle 10: Datenschema Dummycodierung und Covariate
Bedingung |
y - Lernleistung |
x1 |
x2 |
x3 - Lernmotivation |
Methode 1 |
1 2 3 |
1 1 1 |
0 0 0 |
4 4 6 |
Methode 2 |
7 8 6 |
0 0 0 |
1 1 1 |
12 10 10 |
Kontrollgruppe |
5 3 1 |
0 0 0 |
0 0 0 |
14 8 5 |
Tabelle 11: Multiple Regression
|
Multiple R .96658 R Square .93427 Adjusted R Square .89484 Standard Error .84253 |
|||
| Analysis of Variance | |||
| DF | Sum of Squares | Mean Square | |
| Regression | 3 | 50.45070 | 16.81690 |
| Residual | 5 | 3.54930 | .70986 |
| F = 23.69048 Signif F = .0022 |
------------------ Variables in the Equation ------------------
| Variable | B | SE B | Beta | T | Sig T |
| X1 | .830986 | .868821 | .159923 | .956 | .3828 |
| X2 | 3.295775 | .717564 | .634272 | 4.593 | .0059 |
| Motivation | .422535 | .122462 | .588885 | 3.450 | .0182 |
| (Constant) | -.802817 | 1.204732 | -.666 | .5347 |
Die Integration verschiedener statistischer Verfahren durch das allgemeine lineare Modell eröffnet neue Perspektiven bei multivariaten Ansätzen. Für Designs mit ein oder zwei unabhängigen Variablen ist sicherlich nach wie vor die Varianzanalyse vorzuziehen, da für derartig einfache Fragestellungen sich die Interpretation einfacher gestaltet und entsprechende Nachtests (z.B. Scheffé) für den Einzelgruppenvergleich leicht zu rechnen sind. Auch das Problem der Überdeterminierung stellt sich bei ein oder zwei Faktoren noch nicht. Sobald aber die Prädiktorenzahl ansteigt und ein multipler Ansatz gewählt werden muß, bietet sich die multiple Regression geradezu an, um bei Vorhandensein mehrerer Einflußgrößen eine Gewichtung vorzunehmen und außerdem zu ermitteln, ob das Design als Ganzes signifikant ist - ein Schritt, der häufig übersehen wird bei varianzanalytischen Auswertungen. Allerdings setzt die Anwendung des ALM profunde Kenntnisse in Methodenlehre und Statistik voraus, ansonsten ist eine sinnvolle Interpretation der Ergebnisse sowie die Handhabung von Voraussetzungsverletzungen nicht gewährleistet.
Jürgen Bortz (1993). Statistik für Sozialwissenschaftler (4. Auflage). Berlin: Springer Verlag.
Joachim Werner (1997). Lineare Statistik. Weinheim: Beltz Psychologie Verlags Union.